DENSITY 

WHAT IS DENSITY

Denisty is defined as the mass per unit volume.In other words it is the measure of how tightly matter is crammed.Density is temperature dependant and different allotropes of element possess different densities.The greek word for density is "rho".

The formula to calculate density is:

Density(rho)=Mass/Volume 

Si unit: kg/m^3 

COMPARING THE DENSITY OF SOLIDS,LIQUIDS AND GASES 

Particles in a solid are tightly packed together therefore solids have the greatest density.For example Aluminium has a density of 2.643 g/cm^3

The particles in a liquid state are together,but are able to move and slide over one another.For example the density of benzene is 1010 kg/m^3

Gases however have the lowest densities since the particles are spread wide apart and are moving a lot.

The particle theory of matter affects mass,volume,density and viscosity. 

CALCULATING DENSITY 

A solid block has a mass of 500g and a total volume of 100 m^3

Calculate its density in kg/m^3

Mass=0.5kg

Volume=100m^3
since,

Desinty=mass/volume 
0.5/100=0.005 kg/m^3

APPLICATION OF DENSITY IN REAL LIFE

HOW A STEEL SHIP FLOATS ON WATER.

Today most ships are made of steel, and therefore, it is even harder to understand why an aircraft carrier weighing many thousands of tons can float. After all, steel has a weight density (the preferred method for measuring density according to the British system of measures) of 480 pounds per cubic foot, and a density of 7,800 kilograms-per-cubic-meter. By contrast, sea water has a weight density of 64 pounds per cubic foot, and a density of 1,030 kilograms-per-cubic-meter.This difference in density should mean that the carrier would sink like a stone—and indeed it would, if all the steel in it were hammered flat. As it is, the hull of the carrier (or indeed of any sea-worthy ship) is designed to displace or move a quantity of water whose weight is greater than that of the vessel itself. The weight of the displaced water—that is, its mass multiplied by the downward acceleration due to gravity—is equal to the buoyant force that the ocean exerts on the ship. If the ship weighs less than the water it displaces, it will float; but if it weighs more, it will sink.Put another way, when the ship is placed in the water, it displaces a certain quantity of water whose weight can be expressed in terms of Vdg —volume multiplied by density multiplied by the downward acceleration due to gravity. The density of sea water is a known figure, as is g (32 ft or 9.8 m/sec 2 ); thus the only variable for the water displaced is its volume.For the buoyant force on the ship, g will of course be the same, and the value of V will be the same as for the water. In order for the ship to float, then, its density must be much less than that of the water it has displaced. This can be achieved by designing the ship in order to maximize displacement. The steel is spread over as large an area as possible, and the curved hull, when seen in cross section, contains a relatively large area of open space. Obviously, the density of this space is much less than that of water; thus, the average density of the ship is greatly reduced, which enables it to float.

HOOKE'S LAW

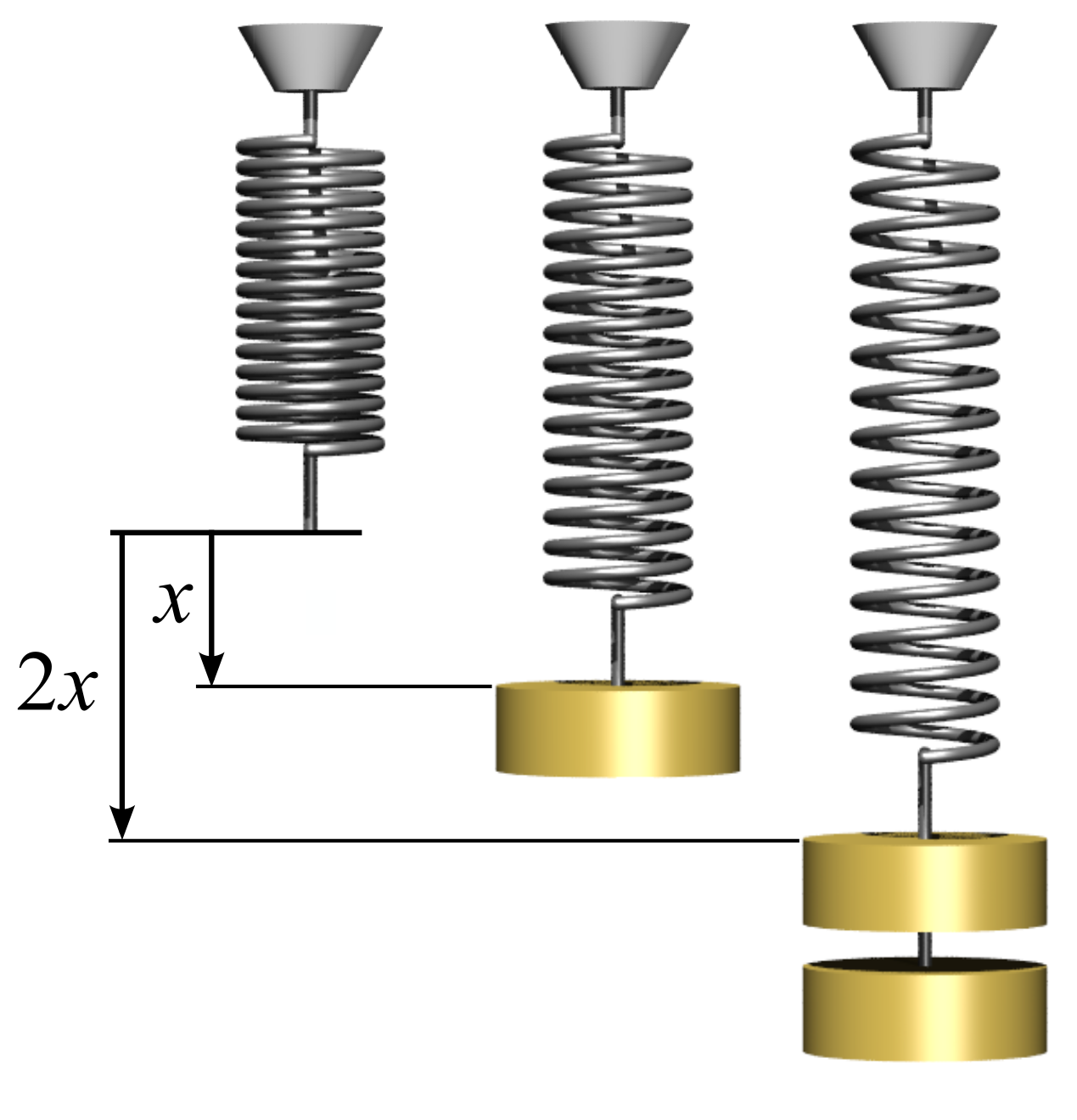
what hookes law actually states is that the force needed to extend or compress a string is directly proportional the distance that is F=kX where 'k' is a constant factor characteristic of the spring.The spring constant k is different for different objects and materials.to find out this we carry out a series of experiment.Different numbers of slotted masses are added onto the spring and its new length is measured at each time.Assuming the limit of proportionality (elastic limit) is not exceeded, a graph of force against extension produces a straight line that passes through the origin.

worked example:

A force of 100 N is stretching a spring by 0.2 m. Calculate the force constant?

Given: Force F = 100 N, 
          Extension x = 0.2 m. 
The force constant is given by k =  Fx 
                                               =  100N0.2m 
                                               =  500 N/m.
 

YOUNG'S MODULUS

What is stress?Could be anything maybe stress related to work or even stress related to job.However when it comes to physics the meaning is completely different to that of our normal day stress.

In physics stress is force per unit area.Since it has the same formula as pressure it has the same units swell,the "Pascals".

Stress= Force/Area

Si units= Pa

strain however is the change in length over the original length.

Strain= change in length/length

since the top and bottom units are same they eliminate eachother leaving us with no units for strain.

m^1-m^-1

=m^1+(-1)

=m^0=1

Now,

The young's modulus is known as stress/strain.

Youngs modulus= F/A divided by change in length/length 

which is equal to ForcexLength/AreaxChange in length 

Si units= Pascals (same as stress since strain itself has no units)

The gradient of the graph of  stress/strain gives us the young's modulus of an object.When calculating the young's modulus in a stress\strain graph always make sure you do it in the region where the spring obeys hooke's law.

Formula for calculating gradient= change in (y)/change in (x)

Worked example:

A crane fitted with a steel cable of uniform diameter 2.3mm and length 28m is used to lift an iron girder of weight 3200N off the ground.

Calculate the extension of the cable when it supports the girder at rest.

The young's modulus for steel= 2.1x10^11 Pa

what we have here is,

Force=3200N

Length=28m

Area of cross section of wire=3.142 x (2.3x10^-3)^2 / 4 =4.15x10^-6 m^2

rearranging the equation for young's modulus gives us

change in length= force x length / area x young's modulus

=3200 x 28/(4.15x10^-6)x(2.1x10^11)

=0.103m

NB:always remember to change mm into metres first since the Si unit of length is metres.

Some important definitions to remember:

Stiffness:The stiffness of different materials ca be compared using the gradient of the stress-strain line which is equal to the young's modulus of the material.

Strength:The strength of a material is its ultimate tensile stress which is its maximum stress.

Brittle: A brittle material snaps without any noticeable yield.For example,glass breaks without any 'give'

Ductile:A ductile material can be drawn into a wire.

STRAIN ENERGY
The elastic energy stored in a stretched wire= 1/2 Force x Change in length

APPLICATIONS OF YOUNGS MODULUS IN REAL LIFE

BONES 
The tensile strength in bone fibers comes from the protein collagen, while the compressive strength is largely due to the presence of inorganic (non-living) salt crystals. It may be hard to believe, but bone actually has an ultimate strength—both in tension and compression—greater than that of concrete!The ultimate strength of most materials is rendered in factors of 10 8 N/m 2 —that is, 100,000,000 newtons (the metric unit of force) per square meter. For concrete under tensile stress, the ultimate strength is 0.02, whereas for bone, it is 1.3. Under compressive stress, the values are 0.2 and 1.7, respectively. In fact, the ultimate tensile strength of bone is close to that of cast iron (1.7), though the ultimate compressive strength of cast iron (5.5) is much higher than for bone.Even with these figures, it may be hard to understand how bone can be stronger than concrete, but that is largely because the volume of concrete used in most situations is much greater than the volume of any bone in the body of a human being. By way of explanation, consider a piece of concrete no bigger than a typical bone: under relatively small amounts of stress, it would crumble.

MATTER AND RADIATION

INSIDE THE ATOM

Atoms are so small that we need an electron microscope on order to see them.every atom contains a nucleus consisting of positively charged protons and neutral neutrons.Surrounding the nucleus are the shells in which the negatively charged electrons orbit.

Some important terms to remember:

• Nucleon number:This shows the total number of protons and neutrons in a nucleus
• Atomic number:Also known as the proton number tells us of the number of protons in an atom.The number of protons and electrons in an atom are the same.
• Ion:A charged particle 

Charge and mass:

                     Mass                          Charge                              Specific charge Q/M

Proton       1.67x10^-27              1.6x10^-19                               9.58x10^7

Electron      9.11x10^-31             -1.6x10^-19                              1.7x10^11

Neutron     1.67x10^-27                     0                                            0

Specific Charge is the charge over its mass.

When we say specific charge of an ion then:

(charge on element)x(proton charge)/(mass of neutron)(mass of proton)(mass of e)

When we say specific charge of a nucleus:

(huber of protons)x(proton charge)/(mass of nucleus)

Example:

Calculate the specific charge of C A=12 Z=6

S.C=C/M

(6)(1.6X10^-19)/(12)(1.67X10^-27)

=4.6X10^7 C/Kg

Note that the electron has the largest specific charge and not the proton.

ISOTOPES

Isotopes are atoms with the same number of protons but different number of neutrons for example C-12 and C-14.They have the same number of protons but different number of neutrons.

Since we know that unlike charges attract and like charges repel so why does the atom not burst since the protons are all positively chagred in the nucleus  but why don't they?there must be a force holding them together.We call this force the strong nuclear force.

It operates inside of the nucleus holding the nucleons together.Its range is about 3-4femtometres and it acts between two protons two neutrons and a proton and neutron.

The force of repulsion that causes the two like protons to repel is the electrostatic force of repulsion.However the strong nuclear force being arguer than the electrostatic force holds the nucleus together.

Consider two protons removing SNF(Strong nuclear force) leaves the electrostatic force between the two protons.As the two protons move away from each other the electrostatic force between then decreases so their energy approaches zero.When the two protons approach each other vey closely the electrostatic force of repulsion causes the protons to enter a state of high energy.

RADIOACTIVITY 

Radioactivity is the disintegration of an unstable nucleus.There are three forms of them:

1. Alpha decay 
2. Beta decay 
3. Gamma decay 

Alpha decay:

• This is a helium nucleus.
• Positively charged.
• can be stopped by paper 

Beta Decay:

• negatively charged 
• Can be stopped by Aluminium 

Gamma Decay:

• Electromagnetic wave
• neutral
• travels at the speed of light 
• can be stopped by Lead  

PHOTONS 

Photons are packet of electromagnetic wave.It is represented by the equation:
E=hf where 'h' is plank's constant 6.63x10^-34Js and 'f' is the frequency.
note:All hot objects emit heat radiation aswell as infrared waves.
The mass of a photon is zero however it does have momentum.The energy of a photon is discrete i.e constant.


EXCITATION AND DE-EXICATION

Exciattion is the process of taking an electron close to the nucleus and placing it into a higher energy level.
E2-E1=hf
Electrons de-excite releasing photons.te photons have a particular energy hence a particular frequency so correspond to a particular colour.
E1-E2=hf


PARTICLES AND ANTIPARTICLES

Every particle in this universe has an antiparticle.An antiparticle has the rest mass as the particle but it has the opposite charge.
When a particle and antiparticle collide their total mass is converted into energy.this process is called annihilation.
In annihilaton:Eo=hf
For example when an electron collides with a positron (antiparticle of electron) they are converted into 2 photons.

In Pair production the photon passes near a nucleus to give back a particle and antiparticle.

In pair production:hf=2Eo

Conclusion:

Mass has be equated to energy as seen by the two processes.In annihilation mass is converted into energy and in pair production energy is converted into mass.

WAVES

A wave can be described as a disturbance that travels through a medium from one location to another location. Waves that require a medium in order to travel are known as mechanical waves.Examples of mechanic waves are sound waves and seismic waves.Electromagnetic waves however do not require a medium to travel.The vibrating electric field generates a vibrating magnetic field,which generates a vibrating electric field further away and so on.Examples of electromagnetic waves are radio waves,infrared radiation,microwaves etc.

 LONGITUDANAL AND TRANSVERSE WAVES

Longitudinal waves are waves in which the direction of the particles is parallel to that of the direction o the wave. Sound waves, primary seismic waves are examples of longitudinal waves. They consist of compressions and rarefactions.

Transverse waves are waves in which the direction of the particles is perpendicular to the direction of the waves.Examples of transverse waves are electromagnetic waves, secondary seismic waves etc. It consists of crests and troughs.

 POLARISATION

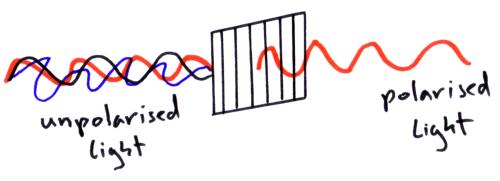
Note:ONLY TRANSVERSE WAVES CAN BE POLARISED.

Unpolarised waves travel in all directions however polarised waves are those which only travel in one direction.Polarisation is the process in which unpolarised waves are converted into polarised waves using polaroids.Examples of unpolarised waves are filament light and also light from candles.

HOW ARE WAVES MEASURED

Key terms to remember:

Displacement of a vibrating particle is its distance and direction from its equilibrium position.

Amplitude of a wave is its maximum displacement.

Wavelength of a wave is one complete wave.(Two points is phase,crest to crest,trough to trough)

Frequency is the number of waves produced in one second

Important Equations:

Speed of a wave=Wavelength x Frequency 

Frequency of a wave=1/time 

PROPERTIES OF WAVES

1. Reflection 
2. Refraction
3. Diffraction 

Reflection

Straight waves directed at a certain angle to a hard flat surface reflect off at the same angle.

Laws of reflection:

1. reflected ray,incident ray and normal all lie on the same surface 
2. angle of incidence is equal to the angle of relection

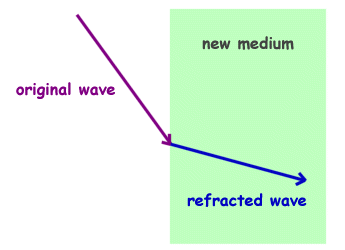
Refraction

When waves across a boundary at which the speed changes,when the wavelength also changes.

Laws of refraction:

1. Normal,incident ray and reflected ray all lie on the same plane
2. Ratio of Sin i over sin r is equal to the refractive index

Diffraction

Diffraction occurs when waves spread out after passing through a gap or round an obstacle.The effect can be seen in a ripple tank when straight waves are directed at a gap.

Note:

1. The narrower the gap,the more the waves spread out.
2. The longer the wavelength,the more the waves spread out.
3. Reducing the gap and increasing the wavelength of the waves will make no change on the diffraction.